Découvrez tous les examens et exercices du Deuxième Trimestre au même endroit!


✅ 1er Année Secondaire
🎯 DC N°2 avec correction
✍️ Ammar bouajila et Chokri Trabelsi

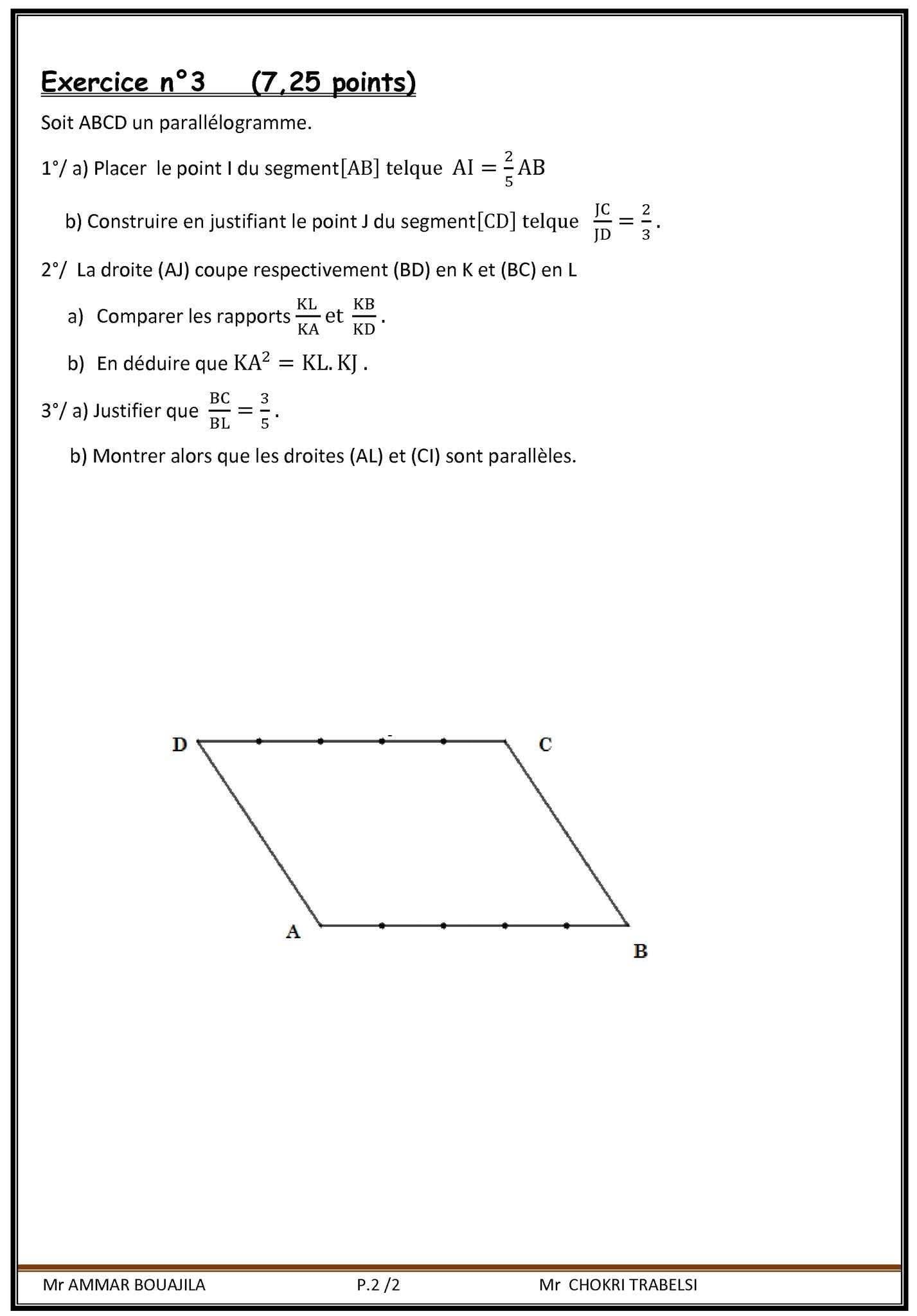
Aucun commentaire pour le moment.
Aucun commentaire pour le moment.

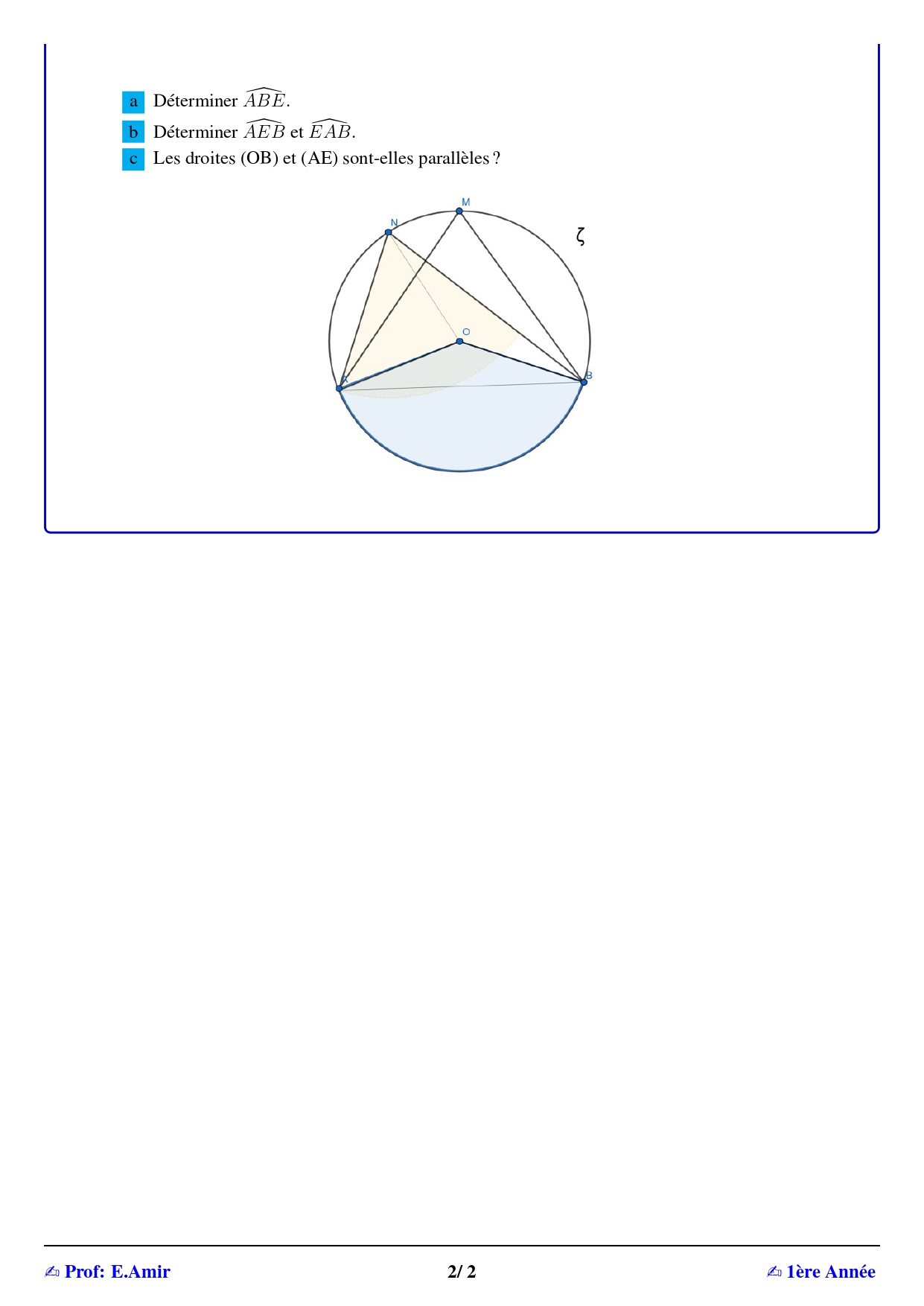
Aucun commentaire pour le moment.
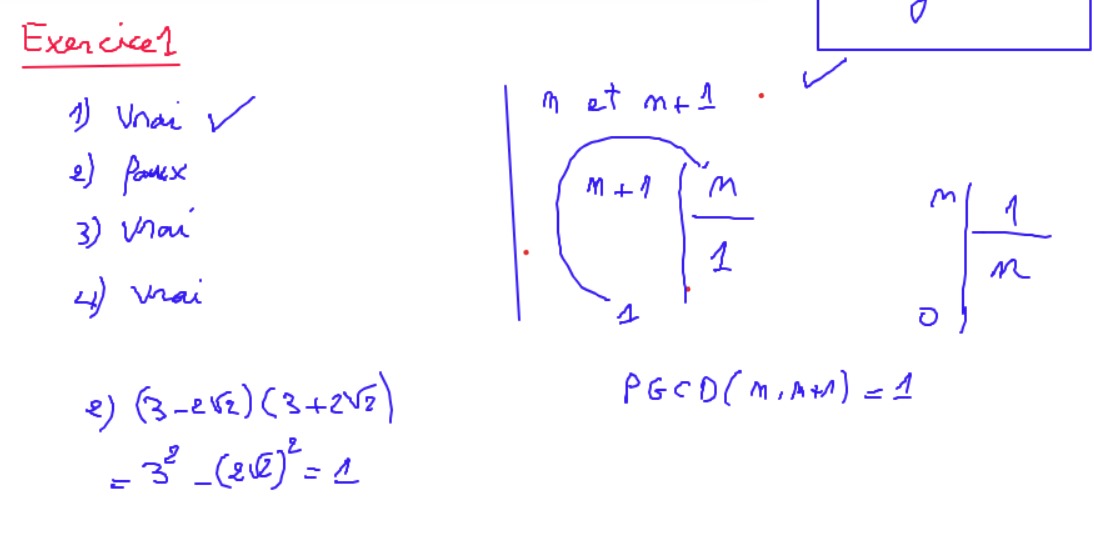
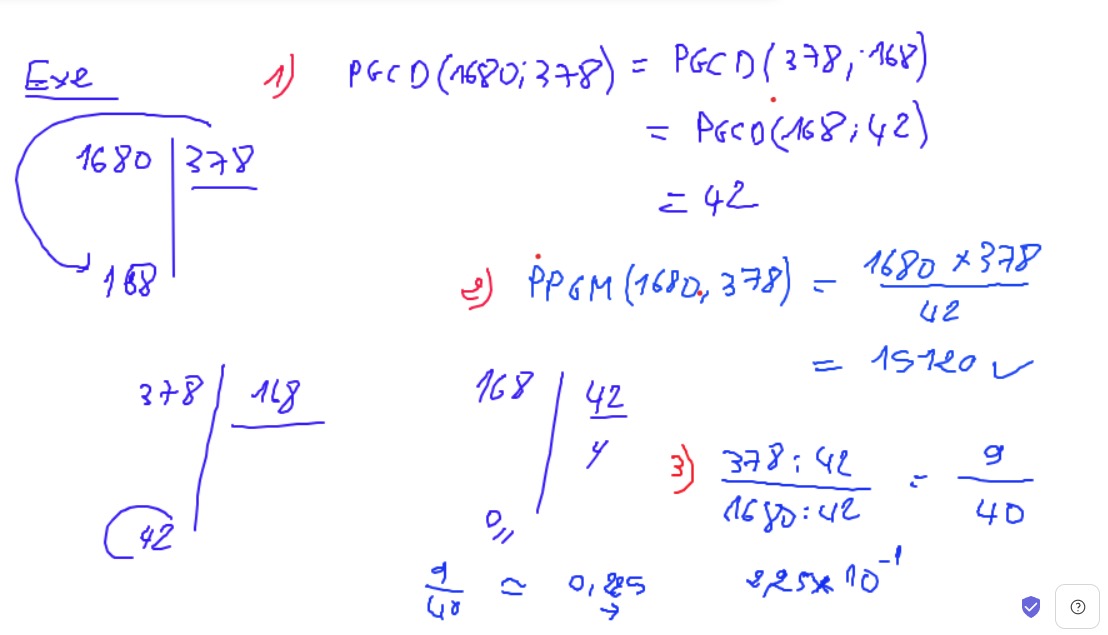
Aucun commentaire pour le moment.

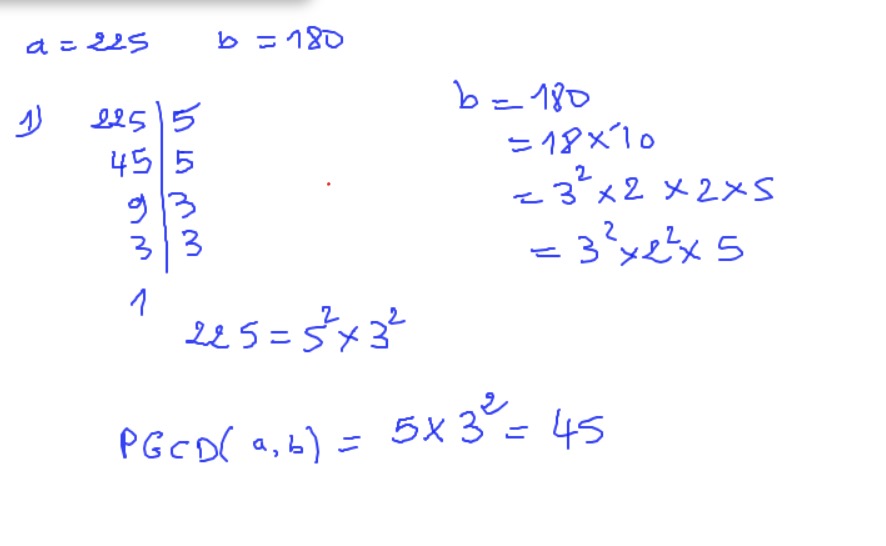
Aucun commentaire pour le moment.
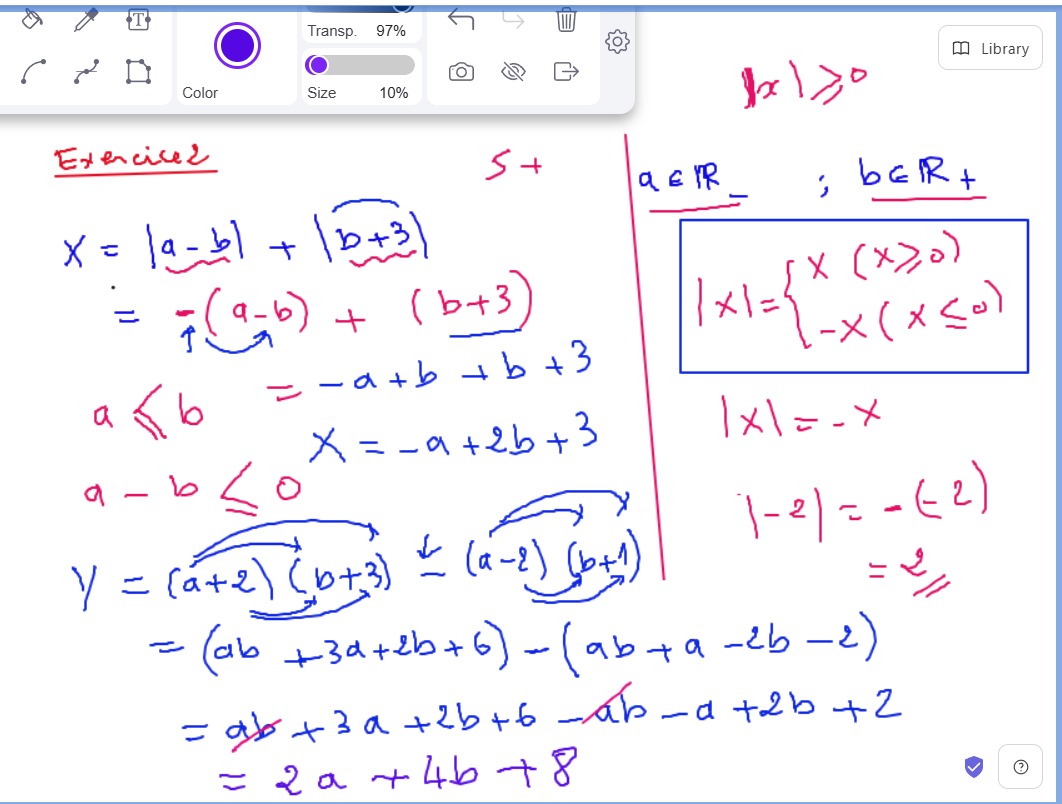
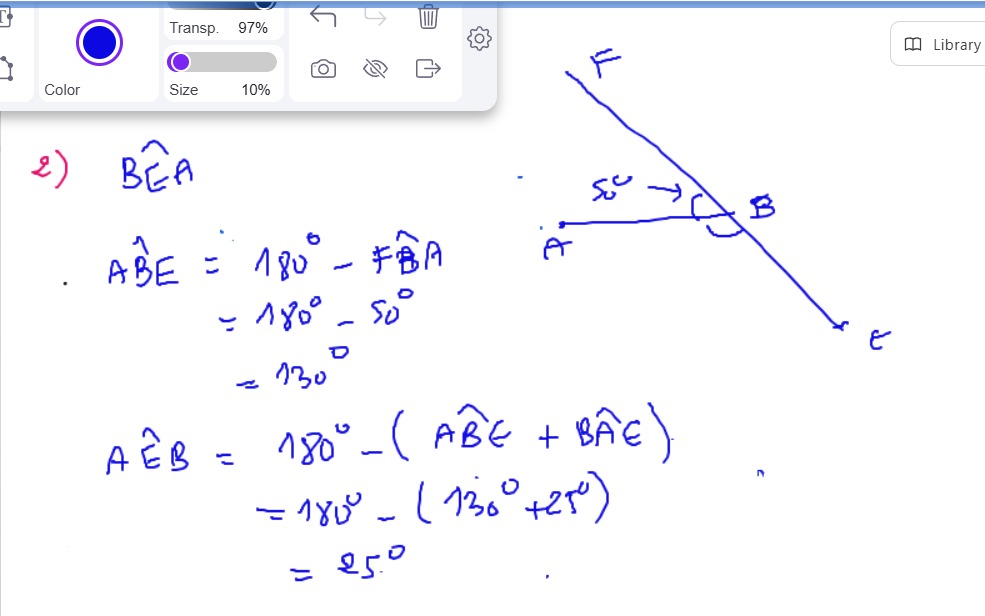
Aucun commentaire pour le moment.


Aucun commentaire pour le moment.


Aucun commentaire pour le moment.


Aucun commentaire pour le moment.


Aucun commentaire pour le moment.


Aucun commentaire pour le moment.


Aucun commentaire pour le moment.

Aucun commentaire pour le moment.


Aucun commentaire pour le moment.

Aucun commentaire pour le moment.


Aucun commentaire pour le moment.


Aucun commentaire pour le moment.


Aucun commentaire pour le moment.
Commentaires
Aucun commentaire pour le moment.